Masonry
publish date: 2024/07/08 19:35:00 UTC
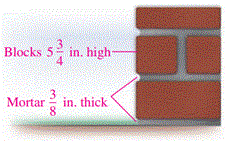
volume_muteTo build a wall, a mason will use blocks that are \(5\frac34\) inches high, held together with \(\frac38\) inch-thick layers of mortar. If the plans call for 8 layers, called course, of blocks, what will be the height of the wall when completed?
Correct Answer
Explanation
Analyze
- The blocks are \(5\frac34\) inches high. (Given)
- The layer of mortar is \(\frac38\) inch thick. (Given)
- There are 8 layers (courses) of blocks. (Given)
- What is the height of the wall when completed? (Find)
From
To find the height of the wall when it is completed, we could add the heights of 8 blocks and 8 layers of mortar. However, it will be simpler if we find the height of one block and one layer of mortar, and multiply that result by 8.
The height of the wall when completed is equal to 8 times (the height of one block plus the thickness of one layer of mortar)
The height of the wall when completed = \(8 \left( 5\frac34 + \frac38 \right)\)
Solve
- Prepare to add the fractions within the parentheses" The LCD is 8. Build \(\frac34\) so that its denominator is 8: \(\frac34 \cdot \frac22 = \frac68\).
- \(8\left(f\frac34 + \frac38 \right) = 8\left(5\frac68 + \frac38 \right)\)
- Add the numerators of the fractions: 6 + 3 = 9. Write the sum over the common denominator 8.
- = \(8\left(5\frac98\right)\)
- Prepare to multiply the fractions. Write \(5\frac98\) as an improper fraction.
- = \(\frac81 \left(\frac{49}{8} \right)\)
- Multiply the numerators and multiply the denominators. To simplify, reomve the common factor of 8 from the numerator and denominator.
- = \(\require{cancel} \frac{\cancel{8}^1 \cdot 49}{1 \cdot \cancel{8}_1}\)
- Simplify: \(\frac{49}{1} = 49\)
- = 49
State
The completed wall will be 49 inches high.
Check
We can estimate to check the result. Since one block and one layer of mortar is about 6 inches high, eight layers of blocks and mortar would be 8 • 6 inches, or 48 inches high. The result of 49 inches seems reasonable.
Reference
Mathematics for college students
